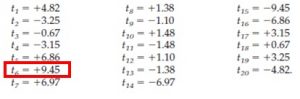Robin Trama, Yoann Blache, Christophe Hautier
Université Claude Bernard Lyon 1, Laboratoire Interuniversitaire de Biologie de la Motricité, Villeurbanne, France
Un peu d’histoire
La cartographie statistique paramétrique (Statistical Parametric Mapping), abrégée SPM, est une méthode d’analyse statistique employée dans le domaine de l’imagerie médicale. Cette méthode a été développée au début des années 1990 (1), et est notamment employée lors d’IRM fonctionnels afin de détecter les zones du cerveau étant sollicitées par une tache. La portabilité de cette analyse au domaine des sciences du sport a été initiée par Pataky dans les années 2010 (2) et a permis de faire des inférences statistiques sur des courbes (1D) ou des cartes (2D).
Les fondements de la SPM
Comme dans les statistiques classiques sur des valeurs extraites (0D), il existe une approche paramétrique et une non-paramétrique à la méthode SPM. La méthode paramétrique se base sur les champs gaussiens aléatoires, qui permet de faire des inférences statistiques sur des courbes. La méthode non-paramétrique quant-à-elle, se base sur des tests de permutations de labels (3), et se base sur du ré-échantillonnage et de l’aléatoire pour effectuer l’inférence statistique. L’avantage principal de l’approche non paramétrique est qu’une distribution gaussienne des données n’est pas requise, ce qui permet de l’adapter aussi bien aux courbes qu’aux cartes.
La permutation de labels
Cette technique statistique a été développée au début des années 1900, mais les ressources informatiques nécessaires à son application plus large manquaient jusque dans les années 1980. En se basant sur le résultat du test statistique, c’est-à-dire la valeur t d’un test t ou la valeur F d’une analyse de variance (ANOVA), et de différentes permutations de labels (« mon résultat est-il plus significatif si ces deux personnes inversent leurs groupes ? »), il est possible de calculer la distribution des données de manière empirique. Prenons l’exemple mis en avant par Nichols & Holmes (3), avec une série de 6 mesures étant organisées sous les labels ABABAB. Si nous testons toutes les permutations possibles de ces labels, nous obtiendront 20 possibilités (Figure 1).
Figure 1: Les 20 labellisations possibles avec 6 mesures
A chacun de ces 20 tests correspond la valeur du test réalisé (ici un test t) (Figure 2). Si le résultat était dû à la chance, la labélisation avec le plus haut (ou bas) score statistique aurait pu être n’importe laquelle des 20 labellisations. Cependant, le résultat avec le plus haut score est bien notre labellisation d’origine, montrant qu’il y avait 1/20 chance que cela se produise. Notre résultat est donc significatif à 1/20, soit 5%. A noter que la situation 15, obtenant le score le plus bas, est simplement une inversion des labels A et B.
Figure 2: Les 20 valeurs du test t pour chacune des labellisations
Cette méthodologie est ensuite appliquée à chaque point (aussi appelé nœud) de la courbe ou de la carte. Le nœud ayant la labellisation avec la plus grande valeur statistique définie la distribution statistique maximale, qui sera utilisée comme référence par la suite. Cette distribution est alors ordonnée de la plus grande à la plus petite valeur. Si nous avons 100 labellisations et un risque de 5%, la 5ème valeur la plus grande représente le seuil des 5%. Pour avoir un risque inférieur à 5% le seuil statistique est défini avec la valeur inférieure à ce risque, soit la 4ème valeur. Par la suite, les valeurs (t ou F) de chaque nœud étant supérieures à ce seuil sont considérées comme significatives. Pour chacun des tests effectués avec des données différentes, un nouveau seuil avec une nouvelle distribution sont calculés. C’est-à-dire que les différents effets d’une ANOVA, ou les différents test t composant le post-hoc n’auront pas le même seuil. Le seuil étant défini par un seul nœud, il est important que les nœuds soient liées, c’est-à-dire qu’ils appartiennent au même mouvement, voire phase d’un mouvement. De plus, il est important d’avoir suffisamment de participants de l’étude pour obtenir un nombre suffisant de permutations afin d’atteindre la précision statistique requise.
La fonction proposée
Cette approche a été proposée, codée, et mise en ligne par Pataky (spm1d.org). Cependant, l’utilisation des fonctions proposées ne permet pas de faire l’analyse des données en 2D de manière automatique. De plus, une erreur assez fréquente est de considérer uniquement la significative du dernier test statistique effectué, et non de l’intersection entre les tests post-hoc et l’ANOVA. En effet, une différence entre deux échantillons peut être significative si et seulement si l’ANOVA l’est au niveaux des mêmes nœuds.
La fonction que nous proposons répond à deux objectifs. 1) permettre de faire des inférences statistiques sur des courbes et des cartes avec une mise en forme uniformisée et 2) simplifier les analyses par comparaisons de moyennes tout en considérant les intersections avec les tests effectués en amont.
Pour interpréter les résultats, des figures directement exploitables pour les présentations et/ou les articles sont créées et très personnalisables en fonction des paramètres d’entrées (Figures 3 et 4). De nombreuses figures sont aussi créées en complément, notamment les différences absolues et relatives, les tailles d’effet avec intervalle de confiance, et la valeur brute du test statistique et de son seuillage.
Un fichier au format Matlab (.mat) est aussi créé pour chacune des familles de test afin de retrouver le nombre de permutations, les zones significatives, les seuils statistiques, et les données utilisées pour refaire les figures. Cependant, de nombreux paramètres existent dans la fonction pour personnaliser les figures en 2D (Figure 3) ou 1D (Figure 4).
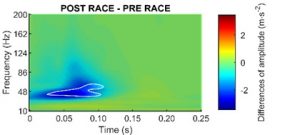
Figure 3: Carte des différences entre 2 conditions expérimentales. La zone plus claire entourée de blanc représente une zone de différences significatives.
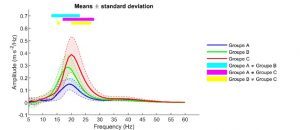
Figure 4: Comparaisons de courbes moyennes avec écart-types sur un continuum fréquentiel. Les barres colorées au sommet de l’image correspondent aux différences significatives pour des comparaisons 2 à 2 (post-hoc).
Obtenir cette fonction
Cette fonction est disponible en libre accès sur différents sites : spm1d.org, GitHub, et FileExchange. N’hésitez pas à faire des tests avec les exemples proposés dans …\fctSPM\Examples pour avoir un aperçu du format des données et des paramètres à renseigner.
En cas de questions ou de problème avec cette fonction, contacter trama.robin@gmail.com.
Mots Clés :
Biomécanique, Statistiques, SPM
Références :
- Friston KJ, Holmes AP, Worsley KJ, Poline JB, Frith CD, Frackowiak RSJ (1995). Statistical parametric maps in functional imaging: a general linear approach.Human Brain Mapping 2, 189–210.
- Pataky TC (2010). Generalized n-dimensional biomechanical field analysis using statistical parametric mapping.Journal of Biomechanics 43, 1976-1982.
- Nichols TE, Holmes AP (2002). Nonparametric permutation tests for functional neuroimaging: a primer with examples.Human Brain Mapping 15, 1–25.
L’auteur du billet
Robin Trama est doctorant au Laboratoire Interuniversitaire de la Biologie de la Motricité (LIBM) de l’Université Claude Bernard Lyon 1. Sa thèse porte sur l’étude des vibrations des tissus mous dans les différentes pratiques sportives, afin de mieux en comprendre les effets sur le système musculosquelettique.
